Department of Computer Science | Institute of Theoretical Computer Science | CADMO
Theory of Combinatorial Algorithms
Prof. Emo Welzl and Prof. Bernd Gärtner
Department of Computer Science | Institute of Theoretical Computer Science | CADMO
Prof. Emo Welzl and Prof. Bernd Gärtner

The best lower bound for deterministic algorithms known so far is 2d-3 where d is the dimension of the unique sink orientation. Tibor Szabó described an idea of how to construct a superlinear lower bound.
Given an arbitrary orientation of a d-dimensional cube, how long will a deterministic algorithm need to either find a sink or prove that the orientation has not the unique sink property?
Pavel Valtr and Jirí Matousek described a method of generating a random unique sink orientation by iteratively flipping edges. This gives rise to a Markov chain.
The mixing rate of the Markov chain is unknown.
Take a face of a random unique sink orientation of fixed dimension. Is this face uniform at random?
Jirí Matousek described the proof for a lower bound of
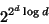 and
announced an upper bound of
and
announced an upper bound of
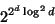
Update: Jirí Matousek announced a matching upper bound of
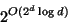 .
.
For i-nice unique sink orientations (i small) Random Edge performs quite well. The question is how small i can be chosen for interesting classes of unique sink orientations (e.g. acyclic orientations).
For a simple 3-polytope P with n facets Random Edge needs
at most
![]() .
.
Update: Micha Sharir improved the upper bound by a constant.
Walter Morris' 3-dimensional P-Cubes are exactly those 3D-USOs which satisfy the Holt-Klee condition, i.e. have 3 knot-disjoint paths from source to sink. Most likely this is just a coincidence. But it might be a nice starting point for studying P-Cubes more closely to check, whether this property holds in general..